Найти площадь фигуры ограниченной линиями заданными уравнениями. Вычислить площадь фигуры примеры

13.09.2020

Из данной статьи вы узнаете, как найти площадь фигуры, ограниченной линиями, используя вычисления с помощью интегралов. Впервые с постановкой такой задачи мы сталкиваемся в старших классах, когда только-только пройдено изучение определенных интегралов и пора приступить к геометрической интерпретации полученных знаний на практике.

Итак, что потребуется для успешного решения задачи по поиску площади фигуры с помощью интегралов:

Умение грамотно строить чертежи;
Умение решать определенный интеграл с помощью известной формулы Ньютона-Лейбница;
Умение «увидеть» более выгодный вариант решения - т.е. понять, как в том или ином случае будет удобнее проводить интегрирование? Вдоль оси икс (OX) или оси игрек (OY)?
Ну и куда без корректных вычислений?) Сюда входит понимание как решать тот иной тип интегралов и правильные численные вычисления.

Алгоритм решения задачи по вычислению площади фигуры, ограниченной линиями:

1. Строим чертеж. Желательно это делать на листке в клетку, с большим масштабом. Подписываем карандашом над каждым графиком название этой функции. Подпись графиков делается исключительно ради удобства дальнейших вычислений. Получив график искомой фигуры, в большинстве случаев будет видно сразу, какие пределы интегрирования будут использованы. Таким образом мы решаем задачу графическим методом. Однако бывает так, что значения пределов дробные или иррациональные. Поэтому, можно сделать дополнительные расчеты, переходим в шагу два.

2. Если явно не заданы пределы интегрирования, то находим точки пересечения графиков друг с другом, и смотрим, совпадает ли наше графическое решение с аналитическим.

3. Далее, необходимо проанализировать чертеж. В зависимости от того, как располагаются графики функций, существуют разные подходы к нахождению площади фигуры. Рассмотрим разные примеры на нахождение площади фигуры при помощи интегралов.

3.1. Самый классический и простой вариант задачи, это когда нужно найти площадь криволинейной трапеции. Что такое криволинейная трапеция? Это плоская фигура, ограниченная осью икс (у = 0) , прямыми х = а, х = b и любой кривой, непрерывной на промежутке от a до b . При этом, данная фигура неотрицательна и располагается не ниже оси абсцисс. В этом случае, площадь криволинейной трапеции численно равна определенному интегралу, вычисляемого по формуле Ньютона-Лейбница:

Пример 1 y = x2 — 3x + 3, x = 1, x = 3, y = 0 .

Какими линиями ограничена фигура? Имеем параболу y = x2 — 3x + 3 , которая располагается над осью ОХ , она неотрицательна, т.к. все точки этой параболы имеют положительные значения. Далее, заданы прямые х = 1 и х = 3 , которые пролегают параллельно оси ОУ , являются ограничительными линиями фигуры слева и справа. Ну и у = 0 , она же ось икс, которая ограничивает фигуру снизу. Полученная фигура заштрихована, как видно из рисунка слева. В данном случае, можно сразу приступать к решению задачи. Перед нами простой пример криволинейной трапеции, которую далее решаем с помощью формулы Ньютона-Лейбница.

3.2. В предыдущем пункте 3.1 разобран случай, когда криволинейная трапеция расположена над осью икс. Теперь рассмотрим случай, когда условия задачи такие же, за исключением того, что функция пролегает под осью икс. К стандартной формуле Ньютона-Лейбница добавляется минус. Как решать подобную задачу рассмотрим далее.

Пример 2 . Вычислить площадь фигуры, ограниченной линиями y = x2 + 6x + 2, x = -4, x = -1, y = 0 .

В данном примере имеем параболу y = x2 + 6x + 2 , которая берет свое начало из-под оси ОХ , прямые х = -4, х = -1, у = 0 . Здесь у = 0 ограничивает искомую фигуру сверху. Прямые х = -4 и х = -1 это границы, в пределах которых будет вычисляться определенный интеграл. Принцип решения задачи на поиск площади фигуры практически полностью совпадает с примером номер 1. Единственное различие в том, что заданная функция не положительная, и все также непрерывная на промежутке [-4; -1] . Что значит не положительная? Как видно из рисунка, фигура, которая заключается в рамках заданных иксов имеет исключительно «отрицательные» координаты, что нам и требуется увидеть и помнить при решении задачи. Площадь фигуры ищем по формуле Ньютона-Лейбница, только со знаком минус в начале.

Статья не завершена.

Переходим к рассмотрению приложений интегрального исчисления. На этом уроке мы разберем типовую и наиболее распространенную задачу вычисления площади плоской фигуры с помощью определенного интеграла . Наконец-то все ищущие смысл в высшей математике – да найдут его. Мало ли. Придется вот в жизни приближать дачный участок элементарными функциями и находить его площадь с помощью определенного интеграла.

Для успешного освоения материала, необходимо:

1) Разбираться в неопределенном интеграле хотя бы на среднем уровне. Таким образом, чайникам для начала следует ознакомиться с уроком Не.

2) Уметь применять формулу Ньютона-Лейбница и вычислять определенный интеграл. Наладить теплые дружеские отношения с определенными интегралами можно на странице Определенный интеграл. Примеры решений . Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа , поэтому актуальным вопросом будут также ваши знания и навыки построения чертежей. Как минимум, надо уметь строить прямую, параболу и гиперболу.

Начнем с криволинейной трапеции. Криволинейной трапеция - это плоская фигура, ограниченная графиком некоторой функции y = f (x ), осью OX и линиями x = a ; x = b .

Площадь криволинейной трапеции численно равна определенному интегралу

У любого определенного интеграла (который существует) есть очень хороший геометрический смысл. На уроке Определенный интеграл. Примеры решений мы говорили, что определенный интеграл – это число. А сейчас пришла пора констатировать еще один полезный факт. С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ . То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры . Рассмотрим определенный интеграл

Подынтегральная функция

задает на плоскости кривую (её при желании можно начертить), а сам определенный интеграл численно равен площади соответствующей криволинейной трапеции.

Пример 1

, , , .

Это типовая формулировка задания. Важнейший момент решения – построение чертежа . Причем, чертеж необходимо построить ПРАВИЛЬНО .

При построении чертежа я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций. С техникой поточечного построения можно ознакомиться в справочном материале Графики и свойства элементарных функций . Там же можно найти очень полезный применительно к нашему уроку материал – как быстро построить параболу.

В данной задаче решение может выглядеть так.

Выполним чертеж (обратите внимание, что уравнение y = 0 задает ось OX ):

Штриховать криволинейную трапецию не будем, здесь очевидно, о какой площади идет речь. Решение продолжается так:

На отрезке [-2; 1] график функции y = x 2 + 2 расположен над осью OX , поэтому:

Ответ: .

У кого возникли трудности с вычислением определенного интеграла и применением формулы Ньютона-Лейбница

обратитесь к лекции Определенный интеграл. Примеры решений . После того, как задание выполнено, всегда полезно взглянуть на чертеж и прикинуть, реальный ли получился ответ. В данном случае «на глазок» подсчитываем количество клеточек в чертеже – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получился, скажем, ответ: 20 квадратных единиц, то, очевидно, что где-то допущена ошибка – в рассматриваемую фигуру 20 клеточек явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

Пример 2

Вычислить площадь фигуры, ограниченной линиями xy = 4, x = 2, x = 4 и осью OX .

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Что делать, если криволинейная трапеция расположена под осью OX ?

Пример 3

Вычислить площадь фигуры, ограниченной линиями y = e - x , x = 1 и координатными осями.

Решение: Выполним чертеж:

Если криволинейная трапеция полностью расположена под осью OX , то её площадь можно найти по формуле:

В данном случае:

Внимание! Не следует путать два типа задач:

1) Если Вам предложено решить просто определенный интеграл без всякого геометрического смысла, то он может быть отрицательным.

2) Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.

На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому, от простейших школьных задачек переходим к более содержательным примерам.

Пример 4

Найти площадь плоской фигуры, ограниченной линиями y = 2x – x 2 , y = -x .

Решение: Сначала нужно выполнить чертеж. При построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы y = 2x – x 2 и прямой y = -x . Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:

Значит, нижний предел интегрирования a = 0, верхний предел интегрирования b = 3. Часто выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Тем не менее, аналитический способ нахождения пределов все-таки приходится иногда применять, если, например, график достаточно большой, или поточенное построение не выявило пределов интегрирования (они могут быть дробными или иррациональными). Возвращаемся к нашей задаче: рациональнее сначала построить прямую и только потом параболу. Выполним чертеж:

Повторимся, что при поточечном построении пределы интегрирования чаще всего выясняются «автоматоматически».

А теперь рабочая формула:

Если на отрезке [a ; b ] некоторая непрерывная функция f (x ) больше либо равна некоторой непрерывной функции g (x ), то площадь соответствующей фигуры можно найти по формуле:

Здесь уже не надо думать, где расположена фигура – над осью или под осью, а важно, какой график ВЫШЕ (относительно другого графика), а какой – НИЖЕ .

В рассматриваемом примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из 2x – x 2 необходимо вычесть –x .

Завершение решения может выглядеть так:

Искомая фигура ограничена параболой y = 2x – x 2 сверху и прямой y = -x снизу.

На отрезке 2x – x 2 ≥ -x . По соответствующей формуле:

Ответ: .

На самом деле, школьная формула для площади криволинейной трапеции в нижней полуплоскости (см. пример №3) – частный случай формулы

Поскольку ось OX задается уравнением y = 0, а график функции g (x ) расположен ниже оси OX , то

А сейчас пара примеров для самостоятельного решения

Пример 5

Пример 6

Найти площадь фигуры, ограниченной линиями

В ходе решения задач на вычисление площади с помощью определенного интеграла иногда случается забавный казус. Чертеж выполнен правильно, расчеты – правильно, но, по невнимательности,… найдена площадь не той фигуры.

Пример 7

Сначала выполним чертеж:

Фигура, площадь которой нам нужно найти, заштрихована синим цветом (внимательно смотрите на условие – чем ограничена фигура!). Но на практике, по невнимательности, нередко решают, что нужно найти площадь фигуры, которая заштрихована зеленым цветом!

Этот пример еще и полезен тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:

1) На отрезке [-1; 1] над осью OX расположен график прямой y = x +1;

2) На отрезке над осью OX расположен график гиперболы y = (2/x ).

Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:

Ответ:

Пример 8

Вычислить площадь фигуры, ограниченной линиями

Представим уравнения в «школьном» виде

и выполним поточечный чертеж:

Из чертежа видно, что верхний предел у нас «хороший»: b = 1.

Но чему равен нижний предел?! Понятно, что это не целое число, но какое?

Может быть, a =(-1/3)? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что a =(-1/4). А если мы вообще неправильно построили график?

В таких случаях приходиться тратить дополнительное время и уточнять пределы интегрирования аналитически.

Найдем точки пересечения графиков

Для этого решаем уравнение:

Следовательно, a =(-1/3).

Дальнейшее решение тривиально. Главное, не запутаться в подстановках и знаках. Вычисления здесь не самые простые. На отрезке

, ,

по соответствующей формуле:

Ответ:

В заключение урока, рассмотрим два задания сложнее.

Пример 9

Вычислить площадь фигуры, ограниченной линиями

Решение: Изобразим данную фигуру на чертеже.

Для поточечного построения чертежа необходимо знать внешний вид синусоиды. Вообще, полезно знать графики всех элементарных функций, а также некоторые значения синуса. Их можно найти в таблице значений тригонометрических функций . В ряде случаев (например, в этом) допускается построение схематического чертежа, на котором принципиально правильно должны быть отображены графики и пределы интегрирования.

С пределами интегрирования здесь проблем нет, они следуют прямо из условия:

– «икс» изменяется от нуля до «пи». Оформляем дальнейшее решение:

На отрезке график функции y = sin 3 x расположен над осью OX , поэтому:

(1) Как интегрируются синусы и косинусы в нечетных степенях, можно посмотреть на уроке Интегралы от тригонометрических функций . Отщипываем один синус.

(2) Используем основное тригонометрическое тождество в виде

(3) Проведем замену переменной t = cos x , тогда: расположен над осью , поэтому:

Примечание: обратите внимание, как берется интеграл от тангенса в кубе, здесь использовано следствие основного тригонометрического тождества

На этом уроке будем учиться вычислять площади плоских фигур , которые называются криволинейными трапециями .

Примеры таких фигур - на рисунке ниже.

С одной стороны, найти площадь плоской фигуры с помощью определённого интеграла предельно просто. Речь идёт о площади фигуры, которую сверху ограничивает некоторая кривая, снизу - ось абсцисс (Ox ), а слева и справа - некоторые прямые. Простота в том, что определённый интеграл функции, которой задана кривая, и есть площадь такой фигуры (криволинейной трапеции).

Для вычисления площади фигуры нам понадобятся:

Определённый интеграл от функции, задающей кривую , которая ограничивает криволинейную трапецию сверху. И здесь возникает первый существенный нюанс: криволинейная трапеция может быть ограничена кривой не только сверху, но и снизу . Как действовать в этом случае? Просто, но это важно запомнить: интеграл в этом случае берётся со знаком минус .
Пределы интегрирования a и b , которые находим из уравнений прямых, ограничивающих фигуру слева и справа: x = a , x = b , где a и b - числа.

Отдельно ещё о некоторых нюансах .

Кривая, которая ограничивает криволинейную трапецию сверху (или снизу) должна быть графиком непрерывной и неотрицательной функции y = f (x ) .

Значения "икса" должны принадлежать отрезку [a , b ] . То есть не учитываются такие, например, линии, как разрез гриба, у которого ножка вполне вписывается в этот отрезок, а шляпка намного шире.

Боковые отрезки могут вырождаться в точки . Если вы увидели такую фигуру на чертеже, это не должно вас смущать, так как эта точка всегда имеет своё значение на оси "иксов". А значит с пределами интегрирования всё в порядке.

Теперь можно переходить к формулам и вычислениям. Итак, площадь s криволинейной трапеции может быть вычислена по формуле

Если же f (x ) ≤ 0 (график функции расположен ниже оси Ox ), то площадь криволинейной трапеции может быть вычислена по формуле

Есть ещё случаи, когда и верхняя, и нижняя границы фигуры - функции, соответственно y = f (x ) и y = φ (x ) , то площадь такой фигуры вычисляется по формуле

. (3)

Решаем задачи вместе

Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).

Пример 1. Ox ) и прямыми x = 1 , x = 3 .

Решение. Так как y = 1/x > 0 на отрезке , то площадь криволинейной трапеции находим по формуле (1):

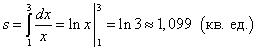Пример 2. Найти площадь фигуры, ограниченной графиком функции , прямой x = 1 и осью абсцисс (Ox ).

Решение. Результат применения формулы (1):

Если то s = 1/2 ; если то s = 1/3 , и т.д.

Пример 3. Найти площадь фигуры, ограниченной графиком функции , осью абсцисс (Ox ) и прямой x = 4 .

Решение. Фигура, соответствующая условию задачи - криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку , по формуле (1) находим площадь криволинейной трапеции:

Пример 4. Найти площадь фигуры, ограниченной линиями , , и находящейся в 1-й четверти.

Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной трапеции ABC . При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A , а для фигуры ABC - абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C - точкой пересечения параболы с осью Ox ). Решая совместно (как систему) уравнения прямой и параболы, получим (абсциссу точки A ) и (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим , (абсциссы точек C и D ). Теперь у нас еть всё для нахождения площади фигуры. Находим:

Пример 5. Найти площадь криволинейной трапеции ACDB , если уравнение кривой CD и абсциссы A и B соответственно 1 и 2.

Решение. Выразим данное уравнение кривой через игрек: Площадь криволинейной трапеции находим по формуле (1):

Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2).

Пример 6. Найти площадь фигуры, ограниченной параболой и осью абсцисс (Ox ).

Решение. Данная фигура расположена ниже оси абсцисс. Поэтому для вычисления её площади воспользуемся формулой (2). Пределами интегрирования являются абсциссы и точек пересечения параболы с осью Ox . Следовательно,

Пример 7. Найти площадь, заключённую между осью абсцисс (Ox ) и двумя соседними волнами синусоиды.

Решение. Площадь данной фигуры можем найти по формуле (2):

Найдём отдельно каждое слагаемое:

Окончательно находим площадь:

Пример 8. Найти площадь фигуры, заключённой между параболой и кривой .

Решение. Выразим уравнения линий через игрек:

Площадь по формуле (2) получим как

где a и b - абсциссы точек A и B . Найдём их, решая совместно уравнения:

Окончательно находим площадь:

И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3).

Пример 9. Найти площадь фигуры, заключённой между параболами и .

Пусть функция неотрицательна и непрерывна на отрезке . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью , слева и справа – прямыми и (см. рис. 2) вычисляется по формуле

Пример 9. Найти площадь фигуры, ограниченной линией и осью .

Решение . Графиком функции является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью (прямой ). Для этого решаем систему уравнений

Получаем: , откуда , ; следовательно, , .

Рис. 3

Площадь фигуры находим по формуле (5):

Если функция неположительна и непрерывна на отрезке , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью , слева и справа – прямыми и , вычисляется по формуле

. (6)

В случае, если функция непрерывна на отрезке и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:

Рис. 4

Пример 10. Вычислить площадь фигуры, ограниченной осью и графиком функции при .

Рис. 5

Решение . Сделаем чертеж (рис. 5). Искомая площадь представляет собой сумму площадей и . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему Получим , . Следовательно:

;

Таким образом, площадь заштрихованной фигуры равна

(кв. ед.).

Рис. 6

Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке функций и ,
а слева и справа – прямыми и (рис. 6). Тогда ее площадь вычисляется по формуле

. (8)

Пример 11. Найти площадь фигуры, ограниченной линиями и .

Решение. Данная фигура изображена на рис. 7. Площадь ее вычислим по формуле (8). Решая систему уравнений находим , ; следовательно, , . На отрезке имеем: . Значит, в формуле (8) в качестве возьмем x , а в качестве – . Получим:

(кв. ед.).

Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.

Рис. 7

Пример 12. Найти площадь фигуры, ограниченной линиями , , .

Решение . Сделаем чертеж (рис. 8). Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью , слева и справа – прямыми и , сверху – графиками функций и . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой на две части (1 – это абсцисса точки пересечения линий и ). Площадь каждой из этих частей находим по формуле (4):

(кв. ед.); (кв. ед.). Следовательно:

(кв. ед.).

Рис. 8

х = j (у )

Рис. 9

В заключение отметим, что если криволинейная трапеция ограничена прямыми и , осью и непрерывной на кривой (рис. 9), то ее площадь находится по формуле

Объем тела вращения

Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке функции , осью , прямыми и , вращается вокруг оси (рис. 10). Тогда объем полученного тела вращения вычисляется по формуле

. (9)

Пример 13. Вычислить объем тела, полученного вращением вокруг оси криволинейной трапеции, ограниченной гиперболой , прямыми , и осью .

Решение . Сделаем чертеж (рис. 11).

Из условия задачи следует, что , . По формуле (9) получаем

Рис. 10

Рис. 11

Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = d , осью Оу и графиком непрерывной на отрезке функции (рис. 12), определяется по формуле

. (10)

х = j (у )

Рис. 12

Пример 14 . Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х 2 = 4у , у = 4, х = 0 (рис. 13).

Решение . В соответствии с условием задачи находим пределы интегрирования: , . По формуле (10) получаем:

Рис. 13

Длина дуги плоской кривой

Пусть кривая , заданная уравнением , где , лежит в плоскости (рис. 14).

Рис. 14

Определение. Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.

Если функция и ее производная непрерывны на отрезке , то длина дуги кривой вычисляется по формуле

. (11)

Пример 15 . Вычислить длину дуги кривой , заключенной между точками, для которых .

Решение . Из условия задачи имеем . По формуле (11) получаем:

4. Несобственные интегралы
с бесконечными пределами интегрирования

При введении понятия определённого интеграла предполага-лось, что выполняются следующие два условия:

а) пределы интегрирования а и являются конечными;

б) подынтегральная функция ограничена на отрезке .

Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным .

Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.

Определение. Пусть функция определена и непрерывна на промежутке , тогда и неограниченной справа (рис. 15).

Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.

Рис. 15

Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:

. (13)

Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.

Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:

, (14)

где с – любая точка интервала . Интеграл сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).

;

г) = [выделим в знаменателе полный квадрат: ] = [замена:

] =

Значит, несобственный интеграл сходится и его значение равно .

В действительности, для того чтобы находить площадь фигуры не надо так уж много знаний по неопределенному и определенному интегралу. Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа , поэтому гораздо более актуальным вопросом будут ваши знания и навыки построения чертежей. В этой связи полезно освежить в памяти графики основных элементарных функций, а, как минимум, уметь строить прямую, и гиперболу .

Криволинейной трапецией называется плоская фигура, ограниченная осью , прямыми , и графиком непрерывной на отрезке функции , которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:

Тогда площадь криволинейной трапеции численно равна определенному интегралу . У любого определенного интеграла (который существует) есть очень хороший геометрический смысл.

С точки зрения геометрии определенный интеграл - это ПЛОЩАДЬ .

То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Например, рассмотрим определенный интеграл . Подынтегральная функция задает на плоскости кривую, располагающуюся выше оси (желающие могут выполнить чертёж), а сам определенный интеграл численно равен площади соответствующей криволинейной трапеции.

Пример 1

Это типовая формулировка задания. Первый и важнейший момент решения - построение чертежа . Причем, чертеж необходимо построить ПРАВИЛЬНО .

При построении чертежа я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом - параболы, гиперболы, графики других функций. Графики функций выгоднее строить поточечно.

В данной задаче решение может выглядеть так.
Выполним чертеж (обратите внимание, что уравнение задает ось ):

На отрезке график функции расположен над осью , поэтому:

Ответ:

После того, как задание выполнено, всегда полезно взглянуть на чертеж и прикинуть, реальный ли получился ответ. В данном случае «на глазок» подсчитываем количество клеточек в чертеже - ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получился, скажем, ответ: 20 квадратных единиц, то, очевидно, что где-то допущена ошибка - в рассматриваемую фигуру 20 клеточек явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

Пример 3

Вычислить площадь фигуры, ограниченной линиями , и координатными осями.

Решение : Выполним чертеж:

Если криволинейная трапеция расположена под осью (или, по крайней мере, не выше данной оси), то её площадь можно найти по формуле:

В данном случае:

Внимание! Не следует путать два типа задач :

Пример 4

Найти площадь плоской фигуры, ограниченной линиями , .

Решение : Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы и прямой . Это можно сделать двумя способами. Первый способ - аналитический. Решаем уравнение:

Значит, нижний предел интегрирования , верхний предел интегрирования .

Этим способом лучше, по возможности, не пользоваться .

Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Тем не менее, аналитический способ нахождения пределов все-таки приходится иногда применять, если, например, график достаточно большой, или поточенное построение не выявило пределов интегрирования (они могут быть дробными или иррациональными). И такой пример, мы тоже рассмотрим.

Возвращаемся к нашей задаче: рациональнее сначала построить прямую и только потом параболу. Выполним чертеж:

А теперь рабочая формула : Если на отрезке некоторая непрерывная функция больше либо равна некоторой непрерывной функции , то площадь фигуры, ограниченной графиками данных функций и прямыми , , можно найти по формуле:

Здесь уже не надо думать, где расположена фигура - над осью или под осью, и, грубо говоря, важно, какой график ВЫШЕ (относительно другого графика), а какой - НИЖЕ .

В рассматриваемом примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из необходимо вычесть

Завершение решения может выглядеть так:

Искомая фигура ограничена параболой сверху и прямой снизу.
На отрезке , по соответствующей формуле:

Ответ:

Пример 4

Вычислить площадь фигуры, ограниченной линиями , , , .

Решение : Сначала выполним чертеж:

Фигура, площадь которой нам нужно найти, заштрихована синим цветом (внимательно смотрите на условие - чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована зеленым цветом!

Этот пример еще полезен и тем, что в нём площадь фигуры считается с помощью двух определенных интегралов.

Действительно :

1) На отрезке над осью расположен график прямой ;

2) На отрезке над осью расположен график гиперболы .

Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:

Как вычислить объем тела вращения с помощью определенного интеграла?

Представьте некоторую плоскую фигуру на координатной плоскости. Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами:

Вокруг оси абсцисс ;

Вокруг оси ординат .

В данной статье будут разобраны оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс.

Начнем с наиболее популярной разновидности вращения.