Для нахождения производной тригонометрической функции нужно пользоваться таблицей производных , а именно производными 6-13.
При нахождении производных простых тригонометрических функций во избежание распространённых ошибок следует обращать внимание на следующие моменты:
- в выражении функции часто одно из слагаемых представляет собой синус, косинус или другую тригонометрическую функцию не от аргумента функции, а от числа (константы), поэтому производная этого слагаемого равна нулю;
- почти всегда нужно упростить выражение, полученное в результате дифференцирования, а для этого нужно уверенно пользоваться знаниями по действиям с дробями;
- для упрощения выражения почти всегда нужно знать тригонометрические тождества, например, формулу двойного угла и формулу единицы как сумму квадратов синуса и косинуса .
Пример 1. Найти производную функции
Решение. Допустим, с производной косинуса всё понятно, скажут многие, начинающие изучать производные. А как быть с производной синуса двенадцати, делённых на пи? Ответ: считать равной нулю! Здесь синус (функция всё-таки!) - ловушка, потому что аргумент - не переменная икс или любая другая переменная, а просто число. То есть, синус этого числа - тоже число. А производная числа (константы), как мы знаем из таблицы производных, равна нулю. Итак, оставляем только минус синус икса и находим его производную, не забывая про знак:
![]() .
.
Пример 2. Найти производную функции
![]() .
.
Решение. Второе слагаемое - тот же случай, что и первое слагаемое в предыдущем примере. То есть, число, а производная числа равна нулю. Находим производную второго слагаемого как производную частного:
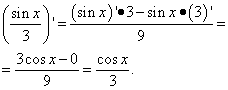
Пример 3. Найти производную функции
Решение. Это уже другая задача: здесь в первом слагаемом нет ни арксинуса, ни другой тригонометической функции, но есть икс, а значит, это функция от икса. Следовательно, дифференцируем её как слагаемое в сумме функций:

Здесь потребовались навыки в действиях с дробями , а именно - в ликвидации трёхэтажности дроби.
Пример 4. Найти производную функции
![]() .
.
Решение. Здесь буква "фи" играет ту же роль, что "икс" в предыдущих случаях (и в большинстве других, но не во всех) - независимой переменной. Поэтому, когда будем искать производную произведения функций, не будем спешить объявлять равной нулю производную корня от "фи". Итак:

Но на этом решение не заканчивается. Так как в двух скобках собраны подобные члены, от нас ещё требуется преобразовать (упростить) выражение. Поэтому умножаем скобки на вынесенные за них множители, а далее приводим слагаемые к общему знаменателю и выполняем другие элементарные преобразования:

Пример 5. Найти производную функции
Решение. В этом примере от нас потребуется знание того факта, что существует такая тригонометрическая функция - секанс - и её формулы через косинус. Дифференцируем:

Пример 6. Найти производную функции
![]() .
.
Решение. В этом примере от нас потребуется помнить из школьного курса формулу двойного угла. Но сначала дифференцируем:

![]() ,
,
(это и есть формула двойного угла)
При
выводе самой первой формулы таблицы
будем исходить из определения
производнойфункции в точке. Возьмем ,
где x
–
любое действительное число, то есть, x
–
любое число из области определения
функции .
Запишем предел отношения приращения
функции к приращению аргумента при :
![]()
Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения .
Производная степенной функции.
Формула
производной степенной функции имеет
вид ![]() ,
где показатель степени p
–
любое действительное число.
,
где показатель степени p
–
любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем
пользоваться определением производной.
Запишем предел отношения приращения
степенной функции к приращению
аргумента:

Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
Следовательно,

Этим доказана формула производной степенной функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним
подстановку в исходный предел:

Если
вспомнить второй
замечательный предел, то придем к
формуле производной показательной
функции:
Производная логарифмической функции.
Докажем
формулу производной логарифмической
функции для всех x
из
области определения и всех допустимых
значениях основания a
логарифма.
По определению производной имеем:

Как
Вы заметили, при доказательстве
преобразования проводились с использованием
свойств логарифма. Равенство  справедливо
в силу второго замечательного предела.
справедливо
в силу второго замечательного предела.
Производные тригонометрических функций.
Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.
По
определению производной для функции
синуса имеем ![]() .
.
Воспользуемся
формулой разности синусов:

Осталось
обратиться к первому замечательному
пределу:

Таким образом, производная функции sin x есть cos x .
Абсолютно
аналогично доказывается формула
производной косинуса.

Следовательно, производная функции cos x есть –sin x .
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса.

Производная обратной функции.
Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, - это производная функции f(x) по x .
Теперь сформулируем правило нахождения производной обратной функции.
Пусть
функции y
= f(x)
и x
= g(y)
взаимно
обратные, определенные на
интервалах и соответственно.
Если в точке существует
конечная отличная от нуля производная
функции f(x)
,
то в точке существует
конечная производная обратной
функции g(y)
,
причем ![]() .
В другой записи
.
В другой записи ![]() .
.
Можно
это правило переформулировать для
любого x
из
промежутка ,
тогда получим  .
.
Давайте проверим справедливость этих формул.
Найдем
обратную функцию для натурального
логарифма ![]() (здесь y
–
функция, а x
-
аргумент). Разрешив это уравнение
относительно x
,
получим (здесь x
–
функция, а y
–
ее аргумент). То есть,
(здесь y
–
функция, а x
-
аргумент). Разрешив это уравнение
относительно x
,
получим (здесь x
–
функция, а y
–
ее аргумент). То есть, ![]() и взаимно
обратные функции.
и взаимно
обратные функции.
Из таблицы
производных видим,
что ![]() и
и ![]() .
.
Убедимся,
что формулы нахождения производных
обратной функции приводят нас к этим
же результатам:

Как видите, получили такие же результаты как и в таблице производных.
Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.
Начнем с производной арксинуса.
![]() .
Тогда по формуле производной обратной
функции получаем
.
Тогда по формуле производной обратной
функции получаем
Осталось провести преобразования.
Так
как областью значений арксинуса является
интервал ![]() ,
то
,
то ![]() (смотрите
раздел основные
элементарные функции, их свойства и
графики). Поэтому ,
а не
рассматриваем.
(смотрите
раздел основные
элементарные функции, их свойства и
графики). Поэтому ,
а не
рассматриваем.
Следовательно, ![]() .
Областью определения производной
арксинуса является промежуток (-1;
1)
.
.
Областью определения производной
арксинуса является промежуток (-1;
1)
.
Для
арккосинуса все делается абсолютно
аналогично:

Найдем производную арктангенса.
Для обратной
функцией является  .
.

Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.
Пусть arctgx
= z
,
тогда

Следовательно,

Схожим
образом находится производная
арккотангенса:

Навигация по странице.
Производная постоянной.
При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем , где x
– любое действительное число, то есть, x
– любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :![]()
Следует заметить, что под знаком предела получается выражение , которое не является , так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения .
Пример.
Найти производные следующих постоянных функций
Решение.
В первом случае мы имеем производную натурального числа 3 , во втором случае нам приходится брать производную от параметра а , который может быть любым действительным числом, в третьем - производную иррационального числа , в четвертом случае имеем производную нуля (ноль является целым числом), в пятом – производную рациональной дроби .
Ответ:
Производные всех этих функций равны нулю для любого действительного x
(на всей области определения)
Производная степенной функции.
Формула производной степенной функции имеет вид ![]() , где показатель степени p
– любое действительное число.
, где показатель степени p
– любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
Для упрощения выражения в числителе обратимся к формуле :
Следовательно,
Этим доказана формула производной степенной функции для натурального показателя.
Следует рассмотреть два случая: при положительных x и отрицательных x .
Сначала будем полагать . В этом случае . Выполним логарифмирование равенства по основанию e
и применим свойство логарифма:
Пришли к неявно заданной функции. Находим ее производную:
Осталось провести доказательство для отрицательных x .
Когда показатель p
представляет собой четное число, то степенная функция определена и при , причем является четной (смотрите раздел ). То есть, ![]() . В этом случае и также можно использовать доказательство через логарифмическую производную.
. В этом случае и также можно использовать доказательство через логарифмическую производную.
Когда показатель p
представляет собой нечетное число, то степенная функция определена и при , причем является нечетной. То есть, ![]() . В этом случае и логарифмическую производную использовать нельзя. Для доказательства формулы
. В этом случае и логарифмическую производную использовать нельзя. Для доказательства формулы ![]() в этом случае можно воспользоваться правилами дифференцирования и правилом нахождения производной сложной функции:
в этом случае можно воспользоваться правилами дифференцирования и правилом нахождения производной сложной функции:
Последний переход возможен в силу того, что если p
- нечетное число, то p-1
либо четное число, либо нуль (при p=1
), поэтому, для отрицательных x
справедливо равенство ![]() .
.
Таким образом, формула производной степенной функции доказана для любого действительного p .
Пример.
Найти производные функций .
Решение.
Первую и третью функцию приведем к табличному виду , используя свойства степени, и применим формулу производной степенной функции:
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним подстановку в исходный предел:
По определению производной для функции синуса имеем ![]() .
.
Воспользуемся формулой разности синусов:
Осталось обратиться к первому замечательному пределу:
Таким образом, производная функции sin x есть cos x .
Абсолютно аналогично доказывается формула производной косинуса.

При решении задач дифференцирования мы будем постоянно обращаться к таблице производных основных функций, иначе зачем мы ее составляли и доказывали каждую формулу. Рекомендуем запомнить все эти формулы, в дальнейшем это сэкономит Вам массу времени.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
II семестр
- Признаки возрастания и убывания функции. Теорема Лагранжа.
Определение возрастающей функции.
Функция y = f(x) возрастает на интервале X, если для любых и ![]() выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Определение убывающей функции.
Функция y = f(x) убывает на интервале X, если для любых и ![]() выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.
выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

Теорема Лагранжа: Воспользуемся геометрическим смыслом производной, чтобы дать наглядные пояснения справедливости того, что существует касательная к графику f в точке с абсциссой с из интервала (а; b), параллельная секущей, проходящей через точки A (a; f (а)), В (b; f (b)).
Рассмотрим прямую l, параллельную АВ и не имеющую общих точек с частью графика, соответствующей промежутку [а; b]. Будем перемещать эту прямую l по направлению к графику f так, чтобы она оставалась параллельной АВ. Зафиксируем положение l 0 этой прямой в момент, когда у нее появятся общие точки с этой частью графика.
 Из рис.1 видно, что любая из таких «первых» общих точек - точка касания прямой l 0 с графиком f. Обозначим абсциссу этой точки через с. Тогда f’(c)=tg α, где α - угол между прямой l 0 и осью абсцисс. Но l||АВ, поэтому угол α равен углу наклона секущей АВ, т. е. Итак, если функция дифференцируема, то на интервале (а; b) найдется такая точка c∈ (а; b) (рис. 2), что
Из рис.1 видно, что любая из таких «первых» общих точек - точка касания прямой l 0 с графиком f. Обозначим абсциссу этой точки через с. Тогда f’(c)=tg α, где α - угол между прямой l 0 и осью абсцисс. Но l||АВ, поэтому угол α равен углу наклона секущей АВ, т. е. Итак, если функция дифференцируема, то на интервале (а; b) найдется такая точка c∈ (а; b) (рис. 2), что ![]()
- Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I.
Достаточные признаки возрастания и убывания функции :
- если функция f(x)в каждой точке интервала (a,b) имеет положительную производную, то сама функция в этом интервале возрастает;
- если функция f(x) в каждой точке интервала (a,b) имеет отрицательную производную, то функция в этом интервале убывает.
Определение . Функция у=f(x) имеет экстремум (максимум или минимум) в точке х=х 0 , если f(x 0) является наибольшим или наименьшим значением функции в некоторой окрестности этой точки.
- Экстремумы функции. Исследование функции на экстремумы по 1 производной.
Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при x 1 < x 2 выполняется неравенство f(x 1) < f (x 2) (f(x 1) > f(x 2)).
Если дифференцируемая функция y = f(x) на отрезке возрастает (убывает), то ее производная на этом отрезке f ¢(x) > 0 (f ¢(x) < 0).
Точка x 0 называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x 0 , для всех точек которой верно неравенство f(x) £ f(x 0) (f(x) ³ f(x 0)).
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.
Необходимые условия экстремума . Если точка xо является точкой экстремума функции f(x), то либо f ¢(x 0) = 0, либо f ¢(x 0) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
По 1-ой производной:
Пусть x 0 - критическая точка. Если f ¢ (x) при переходе через точку x 0 меняет знак плюс на минус, то в точке x 0 функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x 0 экстремума нет.
Необходимые условия экстремума. Если точка x 0 является точкой экстремума функции f(x), то либо f ¢(x 0) = 0, либо f ¢(x 0) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
- Выпуклость графика функции. Точки перегиба.
Выпуклость функции, точки перегиба
Хорда, соединяющая точки M 1 (x 1 , f(x 1)), M 2 (x 2 , f(x 2)) графика функции f(x) задается функцией
y=L(x, x 1 , x 2) = f(x 1) + f(x 2) (*)
Это проверяется подстановкой координат x 1 , x 2 в правую часть.
Определение. Функция f(x) называется выпуклой вверх на , если для "x 1 L(x, x 1 , x 2) = f(x 1) Если f непрерывна на , дважды дифференцируема на (a,b) и f¢¢(x)>0 на (a,b), то f строго выпукла вниз. Доказательство. "a£x 1 Определение. Точка x 0 называется точкой перегиба функции f, если в точке x 0 существует касательная и в некоторой окрестности точки x 0 график f лежит по разные стороны от касательной. Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений. Рассмотрим функцию y=f(x) непрерывную на отрезке . Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках. Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке: 1.Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках. 2.Вычислить значения функции на концах отрезка при x = a, x = b. 3.Из всех полученных значений выбрать наибольшее и наименьшее. 1 a.Найти ОДЗ и точки разрыва функции. b.Найти точки пересечения графика функции с осями координат. 2.Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания. 3.Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости. 4.Найти асимптоты графика функции: а) вертикальные, b) наклонные. 5.На основании проведенного исследования построить график функции. Определение.
Функция F (x) называется первообразной для функции f (x) на данном промежутке, если для любого х из данного промежутка F"(x)= f (x). Пример:
1.Выяснить, является ли функция F (x) = х 3 – 3х + 1 первообразной для функции f(x) = 3(х 2 – 1). Решение: F"(x) = (х 3 – 3х + 1)′ = 3х 2 – 3 = 3(х 2 – 1) = f(x), т.е. F"(x) = f(x), следовательно, F(x)является первообразной для функции f(x). Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом . Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то Свойства неопределённого интеграла, непосредственно следующие из определения: Примеры плоских фигур Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах: где A, B и C - произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором. Уравнение прямой, проходящей через две заданные несовпадающие точки
Уравнение прямой, проходящей через две заданные несовпадающие точки и Параметрические уравнения прямой.
Параметрические уравнения прямой могут быть записаны в виде: Каноническое уравнение прямой
Каноническое уравнение получается из параметрических уравнений делением одного уравнения на другое: Где - координаты Х и Y направляющего вектора прямой, и координаты точки, принадлежащей прямой. Общее уравнение
Ax + By + C ( > 0).
Вектор = (А; В) - нормальный вектор прямой. Частные случаи: 1) By + C = 0 - прямая параллельна оси Ox; 2) Ax + C = 0 - прямая параллельна оси Oy; 3) Ax + By = 0 - прямая проходит через начало координат; 4) y = 0 - ось Ox; 5) x = 0 - ось Oy. Условие параллельности прямых: k 1 = k 2 . Условие перпендикулярности прямых: k 1 ·k 2 = −1. Углом между пересекающимися прямыми на плоскости, называется градусная мера наименьшего из углов, образованных при пересечении этих прямых. Угол между совпадающими или параллельными прямыми считается равным нулю. Угол α между двумя прямыми, заданными уравнениями: y=k1x+b1 (первая прямая) и y=k2x+b2 (вторая прямая), может быть вычислен по формуле (угол отсчитывается от 1й прямой ко 2й против часовой стрелки): tg(α)=(k2-k1)/(1+k1k2) Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости. а) прямая лежит в плоскости; б) прямая и плоскость имеют только одну общую точку; в) прямая и плоскость не имеют ни одной общей точки. Определение. Две плоскости называются параллельными, если они не имеют общих точек. Параллельность плоскостей и обозначается так: || . Рассмотрим признак параллельности двух плоскостей. Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Свойства параллельных плоскостей: Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны. Признаки параллельности прямой и плоскости: 1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости. 2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны. Признаки параллельности плоскостей: 1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. 2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны. Признаки перпендикулярности прямой и плоскости: 1) Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости. 2) Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой. Наклонная к плоскости. Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости. Теорема о трёх перпендикулярах. Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной. Признаки параллельности прямых в пространстве: 1) Если две прямые перпендикулярны одной и той же плоскости, то они параллельны. 2) Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей. Признак перпендикулярности плоскостей: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Теорема об общем перпендикуляре к двум скрещивающимся прямым. Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр. ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Полуплоскости называются гранями, а ограничивающая их прямая --- ребром двугранного угла. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Призма - многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани - параллелограммами, имеющими общие стороны с этими многоугольниками. Виды призм: Прямая призма - призма, у которой все боковые ребра перпендикулярны основанию, в противном случае призма называется наклонной. Площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или высоту). В прямой призме боковые ребра являются высотами. Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра. Объем наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро. Правильная призма - призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. Основания правильной призмы являются правильными многоугольниками. Боковые грани правильной призмы являются равными прямоугольниками. Боковые ребра правильной призмы равны. Правильная призма является прямой. Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником. Площадь боковой поверхности произвольной призмы , где P - периметр перпендикулярного сечения, l - длина бокового ребра. Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию. Объем призмы: V = S основ H Объем прямоугольного параллелепипеда равен произведению площади основания на высоту: V= SH= abc Объем пирамиды равен одной трети произведения площади основания на высоту: где S – площадь основания, H – высота пирамиды. Объем V усеченной пирамиды может быть найден по формуле где H – высота усеченной пирамиды, S1 и S2 – площади ее оснований. Цили́ндр (др.-греч. κύλινδρος - валик, каток) - геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность - поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Сечение цилиндра плоскостью, параллельной его оси, представляет прямоугольник. Осевым сечением называется сечение, которое проходит через ось цилиндра. Площадь боковой поверхности
цилиндра равна произведению длины окружности основания на высоту: S=2π rh Полная площадь поверхности
цилиндра: Сечение цилиндра. Конус - тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Площадь конуса: Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям. Площадь поверхности усеченного конуса: S=π(r12+(r1+ r2) l+ r22) Шар - это тело ограниченное шаровой поверхностью. Сфера (греч. σφαῖρα - шар) - замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Площадь сферы: Площадь сферической части поверхности шарового сектора: , где H – высота сегмента. Цили́ндр (др.-греч. κύλινδρος - валик, каток) - геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Конус: Усеченный конус: V=1/3π h(r 2 +r 1 ·r 2 +r 2 2) Усеченный конус (рис. 1.20)
Объем шарового сегмента: Объем шарового сектора: Свойства: · Параллелепипед симметричен относительно середины его диагонали. · Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. · Противолежащие грани параллелепипеда параллельны и равны. · Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. Представлены производные обратных тригонометрических функций и вывод их формул. Также даны выражения производных высших порядков. Ссылки на страницы с более подробным изложением вывода формул. См. также:
Обратные тригонометрические функции, их графики и формулы
Сначала выведем формулу производной арксинуса. Пусть Поскольку ,
то .
Тогда Точно таким способом можно получить формулу производной арккосинуса. Однако проще воспользоваться формулой, связывающей обратные тригонометрические функции : Более подробно изложение представлено на странице “Вывод производных арксинуса и арккосинуса ”. Там дается вывод производных двумя способами
- рассмотренным выше и по формуле производной обратной функции. Таким же способом найдем производные арктангенса и арккотангенса. Пусть Производная арккотангенса: Пусть Дифференцируя это уравнение, можно найти производные высших порядков. Производная арксинуса n-го порядка имеет следующий вид: Многочлен удовлетворяет дифференциальному уравнению: Производные для арккосинуса получаются из производных для арксинуса с помощью тригонометрической формулы: Пусть .
Мы нашли производную арккотангенса первого порядка: Разложим дробь на простейшие: Дифференцируем раз и приводим дробь к общему знаменателю: Подставляя ,
получим: Таким образом, производную арктангенса n-го порядка можно представить несколькими способами: Пусть теперь .
Применим формулу, связывающей обратные тригонометрические функции: Подставив ,
найдем: Использованная литература:![]()

![]()

![]() , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.
, где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.![]()

![]()
 Если f(x) непрерывна и положительна на , то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x).
Если f(x) непрерывна и положительна на , то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x).

![]() или в общем виде
или в общем виде  где t - производный параметр, ax, ay - координаты x и y направляющего вектора прямой, при этом
где t - производный параметр, ax, ay - координаты x и y направляющего вектора прямой, при этом
![]() ;
; ![]()


 Случаи взаимного расположения прямой и плоскости:
Случаи взаимного расположения прямой и плоскости:
 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.



 Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) - многогранник, основание которого - многоугольник, а остальные грани - треугольники, имеющие общую вершину.
Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) - многогранник, основание которого - многоугольник, а остальные грани - треугольники, имеющие общую вершину.![]()

![]()


![]()


![]()
![]()
 Параллелепи́пед (от греч. παράλλος - параллельный и греч. επιπεδον - плоскость) - призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.
Параллелепи́пед (от греч. παράλλος - параллельный и греч. επιπεδον - плоскость) - призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.
y = arcsin
x
.
Поскольку арксинус есть функция, обратная к синусу, то
.
Здесь y
- функция от x
.
Дифференцируем по переменной x
:
.
Применяем :
.
Итак, мы нашли:
.
.
И предыдущая формула принимает вид:
.
Отсюда
.
.
Тогда
.
Вывод производных арктангенса и арккотангенса
y = arctg
x
.
Арктангенс есть функция, обратная к тангенсу:
.
Дифференцируем по переменной x
:
.
Применяем формулу производной сложной функции :
.
Итак, мы нашли:
.
.
Производные арксинуса
.
Производную первого порядка от арксинуса мы уже нашли:
.
Дифференцируя, находим производную второго порядка:
;
.
Ее также можно записать в следующем виде:
.
Отсюда получаем дифференциальное уравнение, которому удовлетворяют производные арксинуса первого и второго порядков:
.
Производная арксинуса n-го порядка
,
где - многочлен степени .
Он определяется по формулам:
;
.
Здесь .
.
Производная арккосинуса n-го порядка
.
Поэтому производные этих функций отличаются только знаком:
.
Производные арктангенса
.
.
Здесь - мнимая единица, .
.
.
Производная арктангенса n-го порядка
;
.
Производные арккотангенса
.
Тогда производная n-го порядка от арккотангенса отличаются только знаком от производной арктангенса:
.
.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

 Всеволод большое гнездо как правитель
Всеволод большое гнездо как правитель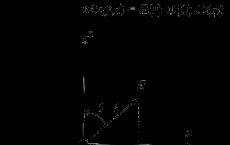 Как заполняются электронные уровни, подуровни и орбитали по мере усложнения атома
Как заполняются электронные уровни, подуровни и орбитали по мере усложнения атома Самые первые спички в мире
Самые первые спички в мире